“ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装”という本で気になったところや理解にくかったところをまとめてます。今回は確率的勾配降下法(stochastic gradient descent)についてです。
勾配法について
勾配法は、ある関数があった時に、その関数を最小にするような変数の値を求める方法です。
式にすると以下のようになります。$\eta$ は学習率を表します。
$$
x_{k+1} = x_k – \eta\frac{\partial f}{\partial x}
$$
以下で簡単な例で確認してみます。
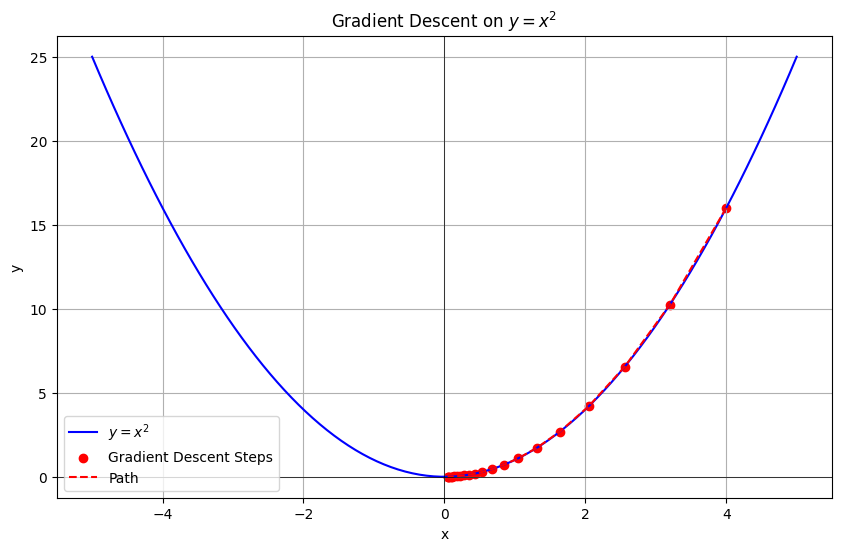
例 : $y=x^2$の最小値を勾配を用いて求める
勾配法(勾配降下法)を用いて $y = x^2$ の最小値を求める方法を説明します。
初期値を$x = 4$、学習率を $\eta = 0.1$と設定して進めていきます。
①微分を求める
関数 $y = x^2$ を微分すると、$\frac{∂y}{∂x}=2x$となります。
②勾配を計算する
初期値 $x = 4$ を先ほど微分した$y’ = 2x$に代入すると、$\frac{∂y}{∂x}=2⋅4=8$
となります。
ここで$x=4$の点で勾配(傾き)が正であったことからx軸の負の方向に移動させると関数が小さくなると分かります。
③学習率 $\eta$ に基づき $x$ を更新
学習率 $\eta = 0.1$ を用いて、現在の勾配に基づく移動量を計算すると以下のようになります。
$$η\frac{∂y}{∂x}=0.1⋅8=0.8$$
よって次のxの値は
$$
x-η\frac{∂y}{∂x}=4-0.8=3.2
$$
となり、次のxは3.2と分かります。
④繰り返す
次のxの値は$3.2$と分かったので、$x=3.2$での$x-\eta\frac{\partial y}{\partial x}$を求めて、次の$x$を更新する。
といったように、勾配を求めて傾きが0となる点を探すまで繰り返すというのが勾配法です。
勾配法の問題点
勾配法にはいくつか問題点があります。
一つ目は、局所解に陥る可能性があるということです。
例えば以下の図を例にとると、赤点では極値となるため傾きは0となりますが、これは最小値ではありません。
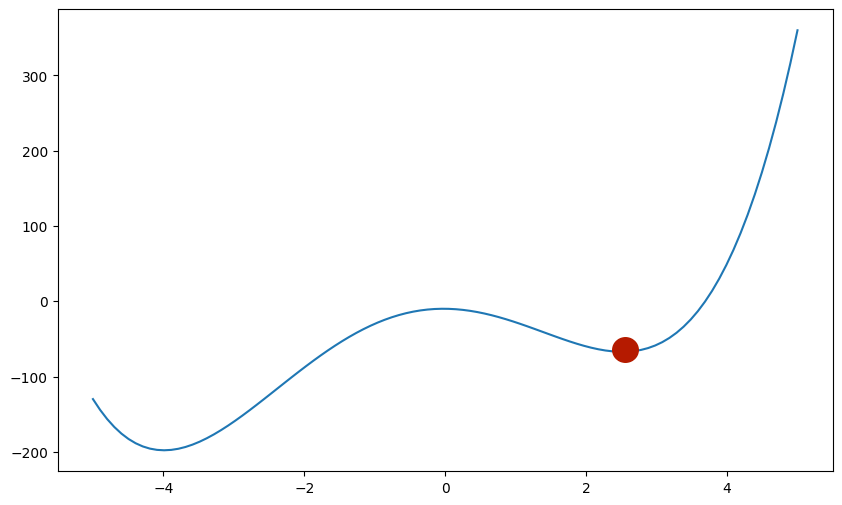
このように、勾配法はより小さい方向に関数を進ませることは出来ますが、そこが最小の値であるとは限りません。
二つ目の問題点は、学習率の大きさです。
学習率$\eta$は大きすぎると一回の移動が大きくなり、最小値を超えてしまい最適解に収束しない可能性があります。
また、反対に小さすぎる場合には繰り返しの回数が多くなり過ぎてしまいます。
このように学習率$\eta$によって学習の安定性にばらつきが生じてしまいます。
確率的勾配降下法について
上記で勾配法とその問題点について挙げました。
その問題点の一つである、局所解に陥ってしまうケースを防ぐ方法の一つが”確率的”という部分です。
ミニバッチ学習
ミニバッチ学習とは、バッチ学習とオンライン学習の中間的な学習手法のことで、データをミニバッチと呼ばれる小さなグループに分けて、順番に処理をしていく学習方法のことです。
例えば、10,000個のデータからランダムに100個を取り出して処理をします。
この際にランダムに取り出す部分が”確率的”となります。
これにより、あるミニバッチでは局所解に陥ってしまっても、他のミニバッチでは局所解とならないといったように勾配降下法の問題点を改善することが出来ます。



コメント